Klassischer Klausuraufbau:

• ER-Diagramm zeichnen
• Relationales Datenbankschema aus ER-Diagramm
• Relationale Algebra, Kalküle
• SQL Queries formulieren zu gegebenen Table
• Funktionale Abhängigkeiten, Normalform
• Synthese, Dekomposition
• Serialisierbarkeit, Nebenläufigkeit, Transaktionsmanagment
• $B^+$-Baum, B-Baum
• XML
• RDF, SPARQL (XPath, XQuery)

Einführung

Ein Datenbanksystem besteht aus:

• Datenbank-Managementsystem (DBMS): Verwaltung der Datenbank; Schnittstelle
• Datenbank (DB): Sammlung aller Daten/Schemata

Big Data Problem: Erfassung, Verarbeitung und Analyse von Daten erfordert immer häufiger effiziente Datenbanksysteme

Entity-Relationship-Modell

Datenbankentwurf

Bestimmung der Struktur und des allgemeinen Aufbaus der Datenbank.

Anforderungsanalyse $\rightarrow$ Entwurf $\rightarrow$ Implementierung $\rightarrow$ Validierung $\rightarrow$ Betrieb ($\rightarrow$ Evolution)

ER-Diagramm

Entity-Typ (Objekt):
Entity-Set (Objektmenge): Menge von konkreten Instanzen des Entity-Typ

Attribute:
Ein Attribut beschreibt die Eigenschaften einer zugehörigen Entity.
Schlüssel:
Einzigartig für eine Instanz.

Ein Attribut kann aus mehreren Attributen bestehen.

Mehrwertige Attribute:

Relationship:

Rekursive Beziehung:

isA Beziehung: partiell:

• Die erbenden Entities decken nur ein Teil der ursprünglichen Entity ab
• Die erbenden Entities spezialisieren alle ursprünglichen Entities

Konzeptueller Entwurf

Relationale Datenmodell

Relationen: $R \subseteq D_1 \times ... \times D_k$ von Domänen z.B. $D_i= \{ 1, ... ,10 \}$ oder $D_j=\{ a,b,c \}$ $\Rightarrow$ $R_{ij} = \{ (1,a), ... , (10,c) \}$
Tupel: $t \in R_{ij}$ Schlüssel: Teilmenge S der Attribute, sodass für Tupel $t_1,t_2$ gilt: $t_1 \neq t_2 \Rightarrow t_1[S] \neq t_2[S]$

Im geordneten Relationenschema spielt ist $(1,a) \neq (a,1)$. Im ungeordneten Relationenschema spielt die Reihenfolge im Tupel keine Rolle.

ER-Diagramm zum relationalen Modell

• Entity-Typ $\rightarrow$ Tabelle/Relation: Student($\underline{\text{MatrNr}}$, Name, Status) - Zusammengesetzte Attribute werden zu einzelnen Attributen

• n:m Beziehungen $\rightarrow$ Relationen für Relation und Entities:

  • Relationen: Entity1($\underline{\text{Key1}}$); Entity2($\underline{\text{Key2}}$); Relationship($\underline{\text{Key1}}, \underline{\text{Key2}}$)
  • Interrelationale Abhängigkeiten: Relationship[Key1] $\subseteq$ Entity1[Key1]; Relationship[Key2] $\subseteq$ Entity2[Key2]
  • Die "Relationship" bekommt Key1 und Key2 als Fremdschlüssel

• 1:n Beziehungen

  • Relationen: Entity1($\underline{\text{Key1}}$, Attr1); Entity2($\underline{\text{Key2}}$, Entity1Key1Relation)
  • Interrelationale Abhängigkeiten: Entity2[Entity1Key1Relation] $\subseteq$ Entity1[Key1]
  • Vorteil: Keine extra Relation für Relation
  • Nachteil: Für Entities die nicht in Beziehung stehen ist Entity1Key1Relation leer

• 1:1 Beziehungen

  • Verschmelzen von 2 Entities zu einer Relation
  • Relationen: Entity1($\underline{\text{Key1}}$, Attr1, Key2 Attr2)

• Rekursive Beziehungen

  • Relationen: Relation($\underline{\text{Vorgänger}}$, $\underline{\text{Nachfolger}}$)
  • Interrelationale Abhängigkeiten: Relation[Vorgänger] $\subseteq$ Entity[Key]; Relation[Nachfolger] $\subseteq$ Entity[Key]

• isA Beziehungen

  • Relationen: Key der Parent-Entity auch für Children-Entity
  • Interrelationale Abhängigkeiten: Children[Key] $\subseteq$ Parent[Key] und Schnittmenge zwischen Children-Relationen ist die leere Menge

• Mehrwertiges Attribut:

  • Aus dem mehwertigen Attribut wird eine Relation
  • Relationen: Entity($\underline{\text{Key}}$, Attr); Mehrwertig($\underline{\text{MehrwertigKey}}$, $\underline{\text{Key}}$)
  • Interrelationale Abhängigkeiten: Mehrwertig[Key] $\subseteq$ Student[Matrkielnummer]

Relationale Algebra

Relationen als Wertebereich. Somit sind R,S Mengen von Tupeln

Grundoperationen

• Vereinigung: $R \cup S$

  • Vereinigt und löscht Duplikate

• Differenz: $R - S$

  • Alle Tupel aus R, welche nicht in S sind

• Kartesisches Produkt: $R \times S$

  • Jedes Tupel aus R verknüpft mit jedem Tupel aus S

• Selektion: $\sigma_F(R)$

  • Selektiert alle Tupel, welche dem boolschen Ausdruck F entsprechen

• Projektion: $\pi_{A_{i_1},...,A_{i_m}}(R)$

  • Gibt nur die Attribute (Spalten) $A_{i_1},...,A_{i_m}$ zurück

• Umbenennung: $\rho_{R'}(R)$ oder $\rho_{A' \leftarrow A}(R)$

  • Bennent Relation R in R' um
  • Bennent Attribut A in A' um für eine Relation R

Alle Grundoperationen sind induktiv definiert, sodass eine Relation auch durch eine gültige Operation auf einer Relation ersetzt werden kann.

Weitere Operationen

• Durchschnitt: $R \cap S = R - (R - S)$

• Natürlicher Verbund (natural join): $R \Join S$

  • Zusammenfügen von Relationen in Abhängigkeit von übereinstimmenden Attributen
  • Funktioniert nur bei gleichen Attributnamen
  • kommutativ und assoziativ

• Theta-Join: $R \Join_{\Theta} S = \sigma_{\Theta}(R \times S)$

  • Nur passende Attribute des Kreuzprodukts
  • Doppelte Attribute werden nicht aussortiert!
• Weitere join operationen

Relationale Kalkül

Deklarative Sprache (im Gegensatz zur prozeduralen Sprache der relationalen Algebra)

Tupelkalkül

Alle Tupel t die die Formel $F(t)$ erfüllen $\{ t | F(t) \}$
z.B. $\{ [p.PersNr] | p \in Professor \land p.Rang = \text{'W3'} \}$

Domänenkalkül

Ein Ausdruck mit k Bereichsvariablen: $\{ x_1,...,x_k | F(x_1,...,x_k) \}$
z.B. $\{ p | \exists n,b (\text{Professor}(p,n,\text{'W3'},b)) \}$

SQL

Structured Query Language ist eine Mischung aus relationaler Algebra und des relationalen Kalküls. SQL ist eine deklarative Datenbankanfragensprache.

CREATE TABLE Cars (
    SerialNumber INTEGER NOT NULL,
    CarName VARCHAR (50),
    OwnerId VARCHAR (50) REFERENCES Owner(OwnerId)
    PRIMARY KEY (SerialNumber)
);

ALTER TABLE Cars
ADD LicencePlate VARCHAR (50);

ALTER TABLE CARs
DROP COLUMN CarName;

CREATE UNIQUE INDEX CarIndex
ON Cars (SerialNumber);

DROP INDEX CarIndex;

// DROP TABLE;

Views

CREATE VIEW OwnedCars AS
SELECT * FROM Cars WHERE OwnerId IS NOT NULL;

Data Manipulation Language

Data Manipulation Language (DML) von SQL

SELECT *                    // Projektion
FROM Cars                   // Kreuzprodukt
WHERE CarName LIKE '%BMW%'  // Selektion

SELECT DISTINCT gibt nur einmalig eine Zeile zurück. Duplikate werden ignoriert.

Aggregatfunktionen

SELECT [COUNT, MIN, MAX, SUM, AVG] ([Distinct] <Attribut>)
FROM ... WHERE ...

COUNT: Anzahl der Zeilen zu gegebener Querry
SUM : Summe der Werte eines Attributs

Gruppieren und Sortieren

SELECT * FROM ...
GROUP BY <Liste von Attributen>
ORDER BY <Liste von Attributen> ASC/DESC

Join

// Theat-Join
SELECT * FROM Cars ...
JOIN ... ON <Bedingung für Attribute>

Es exestieren noch LEFT (OUTER) JOIN, RIGHT (OUTER) JOIN, FULL (OUTER) JOIN, welche analog zu JOIN verwendet werden können. Die funktionsweise lässt sich an der Grafik gut veranschaulichen.

Änderungen

INSERT INTO Cars (CarName, OwnerId)
VALUES ('BMW',1)

DELETE FROM Cars WHERE ...

UPDATE Cars
SET Price = Price + 200
WHERE CarName = %'BMW'%

Relationale Anfragebearbeitung

Günstigsten Auswertungsplan ermitteln.

SQL zu relationaler Algebra (kanonisch)

• Bilde das kartesische Produkt der Relationen
• Führe Selektionen mit den einzelnen Bedingungen durch
• Projeziere auf erforderliche Attribute

Beispiel:

SELECT VName, NName
FROM Studenten AS S, Professoren AS P
WHERE S.NName = P.NName
AND S.Alter < P.Alter - 20

Wird zu:

$\pi_{VName, NName}(\sigma_{S.Alter < P.Alter - 20}(\sigma_{S.NName = P.NName}(S \times P)))$

regelbasierte Anfragenoptimierung

Restrukturierungsalgorithmus

• Aufbrechen der Selektion
• Verschieben der Selektion nach unten
• Kreuzprodukte und Selektionen zu Joins zusammenfassen
• Einfügen und verschieben von Projektionen
• (Zusammenfassen von Selektionen)

Die Idee ist Selektionen möglichst früh durchzuführen und somit eine Performance-Verbesserung zu erreichen.

Indexstrukturen

Prozesse sollen nebenläufig auf Daten arbeiten können. Für sowas verwendet man Festplatten als Sekundärspeicher. Die Daten werden in Blöcken gespeichert.

eindimensionale Daten

Mehrwege-Bäume: Alle Knoten haben $M + 1$ viele Nachfolger ud M viele Schlüssel.

B-Baum: M+1 Mehrwege Suchbaum für eine gerade Zahl M.

• Suchen: Binär vergleichen auf dem jeweiligen Knoten; Suche rekursiv in den Teilbaum. Benötigte Vergleiche: $log_2 M * log_m N$

• Einfügen

  • Passendes Blatt für Objekt suchen
  • Wenn hierdurch das Blatt überläuft, spalte es auf

• Löschen

  • Bei einem Blatt: Lösche Schlüssel aus dem Blatt
  • Bei inneren Knoten: Suche größten Schlüssel links vom zu löschenden Schlüssel. Ersetze den zulöschenden durch den gefundenen Knoten. Lösche den zu löschenden Knoten
  • Bei der Wurzel: So wie bei den anderen beiden, nur darf die Wurzel weniger als M/2 Schlüssel haben

Einfügen:

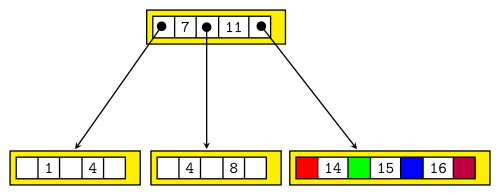
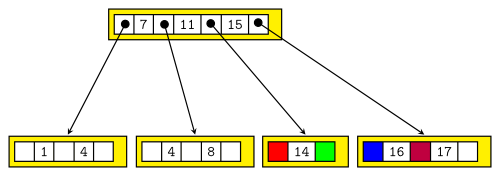
$B^+$-Baum: B-Baum Variante mit zwei Knotentypen

• Blätter enthalten Schlüssel mit Datensätzen oder Verweisen auf Datensätzen

$B^+$-Baum speichert Schlüssel ohne Daten. Dadurch ist der $B^+$-Baum meist breiter und weniger hoch als ein B-Baum.

mehrdimensionale Daten

Invertierte Listen

Quadtree

R-Baum (Rectangel-Baum)

Relationale Entwurfstheorie

Funktionale Abhängigkeiten

Sei $X$ eine Attributmenge und $R$ ein Relationenschema. $\alpha, \beta \subseteq X$.

$\beta$ funktional abhängig von $\alpha$: $\alpha \rightarrow \beta$
intrarelationale Abhängigkeit: $\sigma_K:Rel(X)\rightarrow\{0,1\}$: 1, falls $\alpha \rightarrow \beta$ in R gilt, sonst 0
voll funktional abhängig: Es gilt $\alpha \rightarrow \beta$, aber $\alpha - \{ A \} \nrightarrow \beta$ für alle $A \in \alpha$.
Schlüsselkandidat: Attributmenge $\alpha \subseteq X$ ist ein Schlüsselkandidat, wenn $X$ voll funktional abhängig von $\alpha$ ist
Primärschlüssel: Einer der Schlüsselkandidaten

R erfüllt funktionale Abhängigkeiten $A \rightarrow B$, wenn für Tupel p,q gilt $p.A = q.A$ und $p.B = q.B$

Armstrong Kalkül

implizierte funktionale Abhängigkeiten

Alternative Datenmodelle

Transaktionsverwaltung